by Alberto Martinez

It is well known that you cannot divide a number by zero. Math teachers write, for example, 24 ÷ 0 = undefined. They use analogies to convince students that it is impossible and meaningless, that “you cannot divide something by nothing.” Yet we also learn that we can multiply by zero, add zero, and subtract zero. And some teachers explain that zero is not really nothing, that it is just a number with definite and distinct properties. So, why not divide by zero? In the past, many mathematicians did.
In 628 CE, the Indian mathematician and astronomer Brahmagupta claimed that “zero divided by a zero is zero.” At around 850 CE, another Indian mathematician, Mahavira, more explicitly argued that any number divided by zero leaves that number unchanged, so then, for example, 24 ÷ 0 = 24. Later, around 1150, the mathematician Bhaskara gave yet another result for such operations. He argued that a quantity divided by zero becomes an infinite quantity. This idea persisted for centuries, for example, in 1656, the English mathematician John Wallis likewise argued that 24 ÷ 0 = ∞, introducing this curvy symbol for infinity. Wallis wrote that for ever smaller values of n, the quotient 24 ÷ n becomes increasingly larger (e.g., 24 ÷ .001 = 24,000), and therefore he argued that it becomes infinity when we divide by zero.
The common attitude toward such old notions is that past mathematicians were plainly wrong, confused or “struggling” with division by zero. But that attitude disregards the extent to which even formidably skilled mathematicians thoughtfully held such notions. In particular, the Swiss mathematician, Leonhard Euler, is widely admired as one of the greatest mathematicians in history, having made extraordinary contributions to many branches of mathematics, physics, and astronomy in hundreds of masterful papers written even during his years of blindness. Euler’s Complete Introduction to Algebra (published in German in 1770) has been praised as the most widely published book in the history of algebra. We here include the pages, in German and from an English translation, in which Euler discussed division by zero. He argued that it gives infinity.

A common and reasonable view is that despite his fame, Euler was clearly wrong because if any number divided by zero gives infinity, then all numbers are equal, which is ridiculous. For example:
if 3 ÷ 0 = ∞, and 4 ÷ 0 = ∞,
then ∞ x 0 = 3, and ∞ x 0 = 4.
Here, a single operation, ∞ x 0, has multiple solutions, such that apparently 3 = 4. This is absurd, so one might imagine that there was something “pre-modern” in Euler’s Algebra, that the history of mathematics includes prolonged periods in which mathematicians had not yet found the right answer to certain problems. However, Euler had fair reasons for his arguments. Multiple solutions to one equation did not seem impossible. Euler argued, for one, that the operation of extracting roots yields multiple results. For example, the number 1 has three cube roots, any of which, multiplied by itself three times, produces 1. Today all mathematicians agree that root extraction can yield multiple results.

So why not also admit multiple results when multiplying zero by infinity?
An alternate way to understand the historical disagreements over division by zero is to say that certain mathematical operations evolve over time. In antiquity, mathematicians did not divide by zero. Later, some mathematicians divided by zero, obtaining either zero or the dividend (e.g., that 24 ÷ 0 = 24). Next, other mathematicians argued, for centuries, that the correct quotient is actually infinity. And nowadays again, mathematicians teach that division by zero is impossible, that it is “undefined.” But ever since the mid-1800s, algebraists realized that certain aspects of mathematics are established by convention, by definitions that are established at will and occasionally refined, or redefined. If so, might the result of division by zero change yet again?
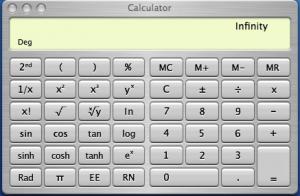
In 2005, I showed students at UT how the computer in our classroom, an Apple iMac, carried out division. I typed 24 ÷ 0, then the enter key. The computer replied “infinity!” Strange that it included an exclamation mark. Some students complained that the computer was an Apple instead of a Windows PC. The following year, a similar Apple computer, a newer model, also answered “infinity,” but without the exclamation mark. In 2010, the same operation on a newer computer in the classroom replied: “DIV BY ZERO.” Yet that same computer has an additional calculator, a so-called scientific calculator, and the same operation on this more sophisticated calculator gave “infinity.”

Students’ calculators, such as in their cell phones, gave other results: “error,” or “undefined.” One student’s calculator, a Droid cell phone, answered: “infinity.” None of these answers is an accident, each has been thoughtfully programmed into each calculator by mathematically trained programmers and engineers. Computer scientists confront the basic and old algebraic problem: using variables and arithmetical operations, occasionally computers encounter a division in which the divisor has a value of zero—what should computers do then? Stop, break down?
On 21 September 1997, the USS Yorktown battleship was testing “Smart Ship” technologies on the coast of Cape Charles, Virginia. At one point, a crew member entered a set of data that mistakenly included a zero in one field, causing a Windows NT computer program to divide by zero. This generated an error that crashed the computer network, causing failure of the ship’s propulsion system, paralyzing the cruiser for more than a day.
These issues show that we are unjustified in assuming that we are lucky enough to live in an age when all the basic operations of mathematics have been settled, when the result of division by zero in particular cannot change again. Instead, when we look at pages from old math books, such as Euler’s Algebra, we should be reminded that some parts of mathematics include operations and concepts involving ambiguities that admit reasonable disagreements. These are not merely mistakes, but instead, plausible alternative directions that mathematics has previously taken and still might take. After all, other operations that seemed impossible for centuries, such as subtracting a greater number from a lesser, or taking roots of negative numbers, are now common. In mathematics, sometimes the impossible becomes possible, often with good reason.

Want to know more about negative numbers?
Alberto A. Martinez, Negative Math: How Mathematical Rules Can Be Positively Bent



